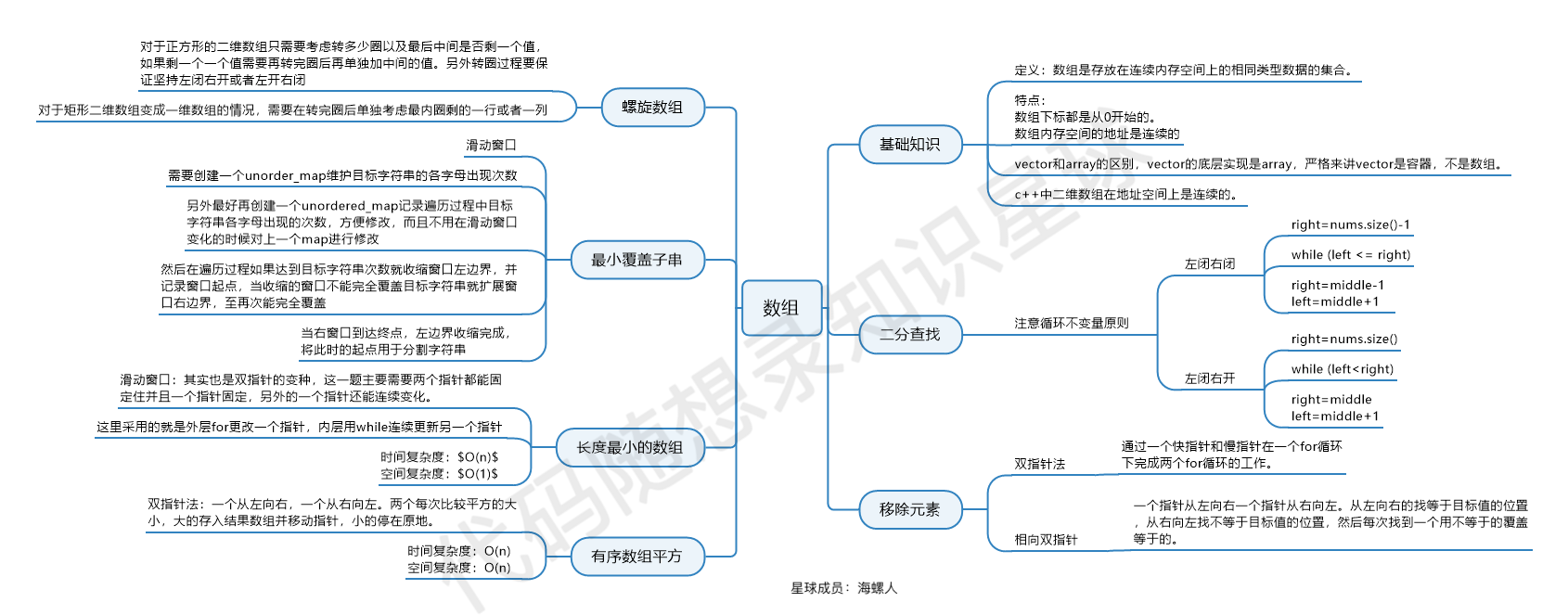
数组

704. 二分查找

力扣链接

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

思路

视频：二分法

这道题的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的。二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边 界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

二分法的区间一般为两种，左闭右闭即**[left, right]，或者左闭右开即[left, right)**。

左闭右闭

定义 target 在左闭右闭的区间里，**也就是[left, right] **。

代码如下：

// 版本一
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

左闭右开

定义 target 在一个在左闭右开的区间里，也就是**[left, right)** 。

代码如下：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

27. 移除元素

力扣题目链接

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。

示例 1:
给定 nums = [3,2,2,3], val = 3,
函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。

示例 2:
给定 nums = [0,1,2,2,3,0,4,2], val = 2,
函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

思路

有的同学可能说了，多余的元素，删掉不就得了。

要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。

暴力求解

• 时间复杂度：

• 空间复杂度：

class Solution{
public:
  int removeElement(vector<int>& nums, int val) {
    int size = nums.size();
    for(int i = 0; i < size; i++){
      if(nums[i] == val){ // 发现需要移除的元素就将后面所有元素向前移一位
        for(int j = i + 1; j < size; j++){
          nums[j - 1] = nums[j];
        }
        i--; // 删除当前的i，后面的依次补上来，在判断下一个顶替是不是等于val，所以要-1
        size--; // 数组的大小变小
    }
    return size;                           
  }
};

快慢指针

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

• 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
• 慢指针：指向更新 新数组下标的位置

删除过程如下：快慢指针同时向前移动，然后再判断快指针是不是等于val。

• 时间复杂度：
• 空间复杂度：

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slow = 0;
        for (int fast = 0; fast < nums.size(); fast++){
            if (val != nums[fast]){
                nums[slow] = nums[fast];
                slow++;
            }
        }
        return slow;
        cout << nums.size()<<endl;
    }
};

977.有序数组的平方

力扣题目链接

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

• 输入：nums = [-4,-1,0,3,10]
• 输出：[0,1,9,16,100]
• 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

示例 2：

• 输入：nums = [-7,-3,2,3,11]
• 输出：[4,9,9,49,121]

暴力排序

最直观的想法，莫过于：每个数平方之后，排个序，美滋滋，代码如下：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        for (int i = 0; i < A.size(); i++) {
            A[i] *= A[i];
        }
        sort(A.begin(), A.end()); // 快速排序
        return A;
    }
};

时间复杂度: ， 可以说是O(nlogn)的时间复杂度。

双指针法

数组其实是有序的， 只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

如动画所示：

写出如下代码：

• 时间复杂度：

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int i = 0;
        int j = A.size() - 1; 
        int k = j;
        vector<int> result(A.size(), 0); // 新建长度与A相同的新数组
        while (i <= j) // 注意这里要i <= j，因为最后要处理两个元素
        {
            if(A[i] * A[i] > A[j] * A[j]){
                result[k--] = A[i] * A[i];
                i++;
            } else {
                result[k--] = A[j] * A[j];
                j--;
            }
        }
        return result;
    }
};

相对于暴力排序的解法O(n + nlog n)还是提升不少的。

209.长度最小的子数组

力扣题目链接

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

• 输入：s = 7, nums = [2,3,1,2,4,3]
• 输出：2
• 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

暴力解法

两个for循环，然后不断的寻找符合条件的子序列

• 时间复杂度：

• 空间复杂度：

代码如下：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX; // 最终的结果
        int sum = 0; // 子序列的数值之和
        int subLength = 0; // 子序列的长度
        for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
            sum = 0;
            for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
                sum += nums[j];
                if (sum >= s) { // 一旦发现子序列和超过了s，更新result
                    subLength = j - i + 1; // 取子序列的长度
                    result = result < subLength ? result : subLength;
                    break; // 因为是找符合条件最短的子序列，所以一旦符合条件就break
                }
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

滑动窗口

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。

但如果只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。

那么滑动窗口的起始位置如何移动呢？

这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：

在本题中实现滑动窗口，主要确定如下三点：

• 窗口内是什么？

  • 满足其和 ≥ s 的长度最小的连续子数组。

• 如何移动窗口的起始位置？

  • 如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

• 如何移动窗口的结束位置？

  • 窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

解题的关键在于 窗口的起始位置如何移动，如图所示：

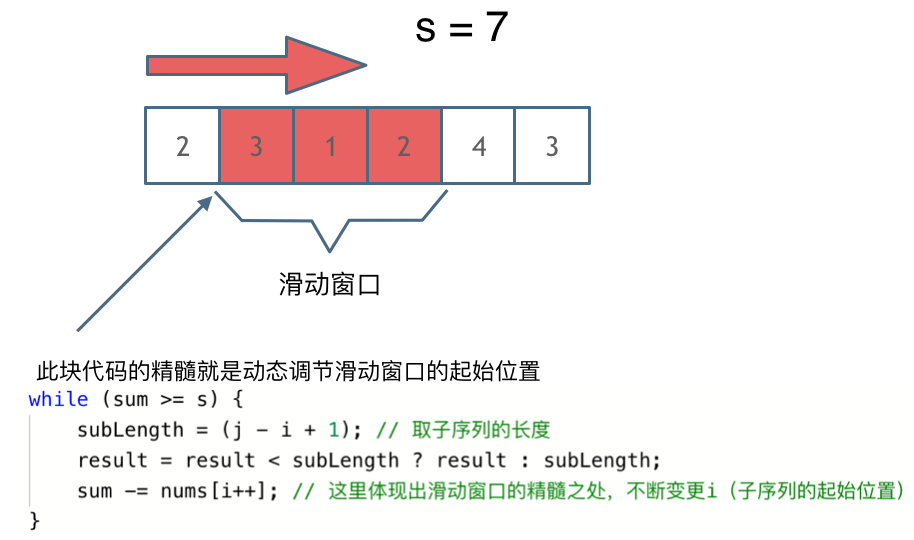
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将暴力解法降为。

C++代码如下：

class Solution {
public:
    int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

一些录友会疑惑为什么时间复杂度是O(n)。

不要以为for里放一个while就以为是O(n^2)啊， 主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。

59.螺旋矩阵II

力扣题目链接

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:

输入: 3
输出:
[
[ 1, 2, 3 ],
[ 8, 9, 4 ],
[ 7, 6, 5 ]
]

思路

大家还记得在这篇文章数组：每次遇到二分法，都是一看就会，一写就废中讲解了二分法，提到如果要写出正确的二分法一定要坚持循环不变量原则。

而求解本题依然是要坚持循环不变量原则。

模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

由外向内一圈一圈这么画下去。

可以发现这里的边界条件非常多，在一个循环中，如此多的边界条件，要画每四条边，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。

那么我按照左闭右开的原则，来画一圈，大家看一下：

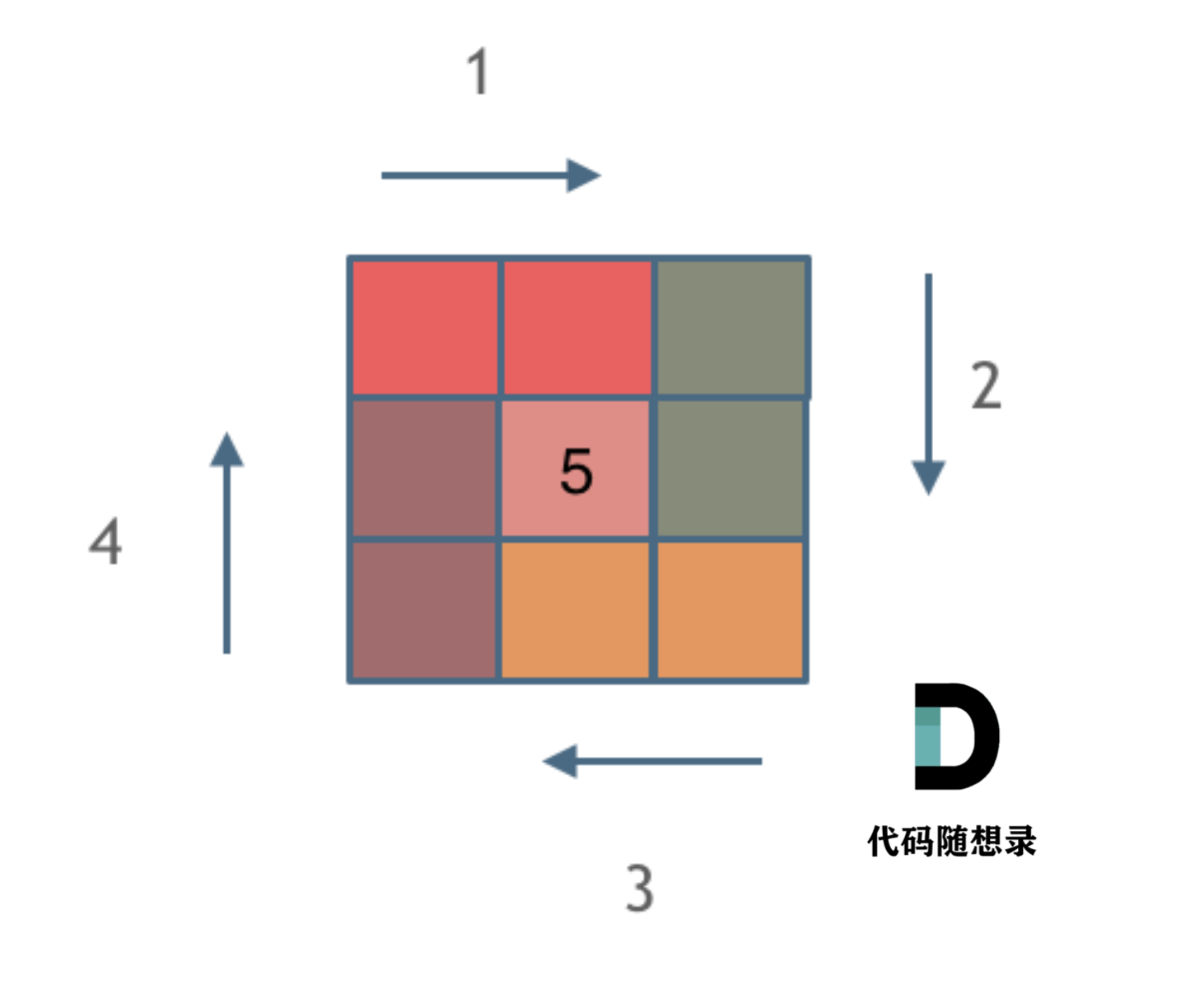
这里每一种颜色，代表一条边，遍历的长度，可以看出每一个拐角处的处理规则，拐角处让给新的一条边来继续画。

这也是坚持了每条边左闭右开的原则。

整体C++代码如下：

• 时间复杂度 : 模拟遍历二维矩阵的时间
• 空间复杂度

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
        int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
        int loop = n / 2; // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
        int mid = n / 2; // 矩阵中间的位置，例如：n为3， 中间的位置就是(1，1)，n为5，中间位置为(2, 2)
        int count = 1; // 用来给矩阵中每一个空格赋值
        int offset = 1; // 需要控制每一条边遍历的长度，每次循环右边界收缩一位
        int i,j;
        while (loop --) {
            i = startx;
            j = starty;

            // 下面开始的四个for就是模拟转了一圈
            // 模拟填充上行从左到右(左闭右开)
            for (j = starty; j < n - offset; j++) {
                res[startx][j] = count++;
            }
            // 模拟填充右列从上到下(左闭右开)
            for (i = startx; i < n - offset; i++) {
                res[i][j] = count++;
            }
            // 模拟填充下行从右到左(左闭右开)
            for (; j > starty; j--) {
                res[i][j] = count++;
            }
            // 模拟填充左列从下到上(左闭右开)
            for (; i > startx; i--) {
                res[i][j] = count++;
            }

            // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            startx++;
            starty++;

            // offset 控制每一圈里每一条边遍历的长度
            offset += 1;
        }

        // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
        if (n % 2) {
            res[mid][mid] = count;
        }
        return res;
    }
};

另一种思路

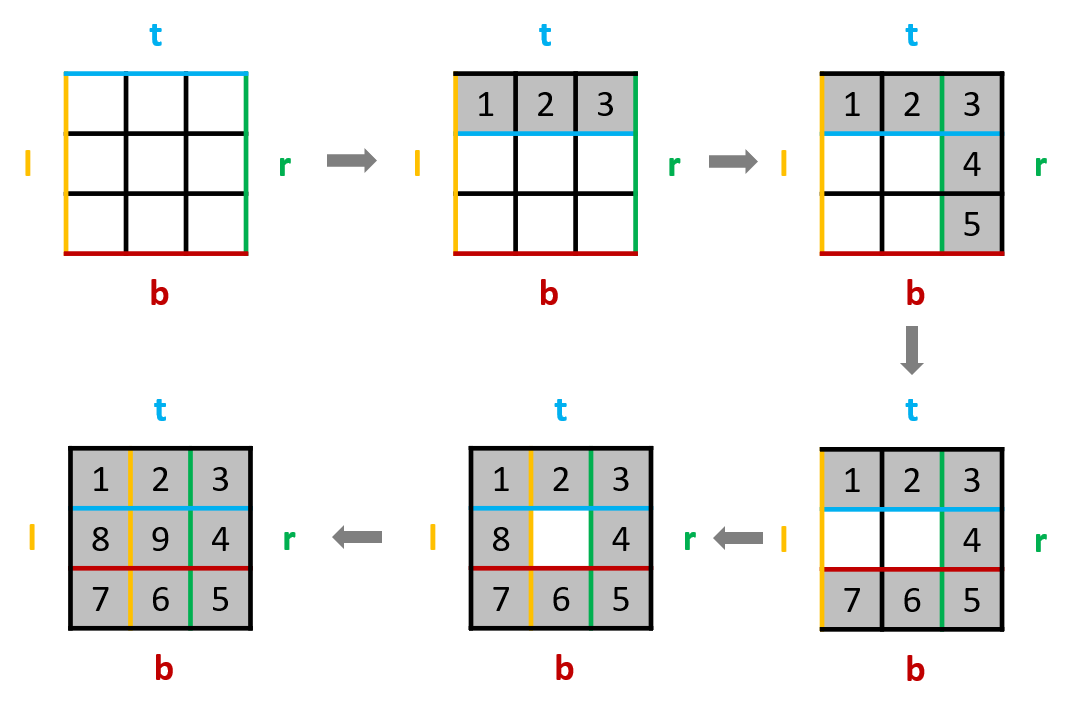
• 生成一个 n×n 空矩阵 mat，随后模拟整个向内环绕的填入过程：

  • 定义当前左右上下边界 l,r,t,b，初始值 num = 1，迭代终止值 tar = n * n；

  • 当 num <= tar 时，始终按照 从左到右 从上到下 从右到左 从下到上 填入顺序循环，每次填入后：

    • 执行 num += 1：得到下一个需要填入的数字；
    • 更新边界：例如从左到右填完后，上边界 t += 1，相当于上边界向内缩 1。

  • 使用num <= tar而不是l < r || t < b作为迭代条件，是为了解决当n为奇数时，矩阵中心数字无法在迭代过程中被填充的问题。

• 最终返回 mat 即可。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int num = 1;
        int left = 0, top = 0, right = n - 1, bottom = n - 1;
        vector<vector<int>>res(n, vector<int>(n, 0));

        while (num <= n*n) {
            // 左→右 填充列
            for (int i = left; i <= right; i++) res[top][i] = num++;
            top++;

            // 上→下 填充行
            for (int i = top; i <= bottom; i++) res[i][right] = num++;
            right--;
            
            // 右→左 填充列
            for (int i = right; i >= left; i--) res[bottom][i] = num++;
            bottom--;
            
            // 下→上 填充行
            for (int i = bottom; i >= top; i--) res[i][left] = num++;
            left++;
        }
        return res; //别忘了返回值！
    }
};

数组总结

数组理论基础

数组是非常基础的数据结构，在面试中，考察数组的题目一般在思维上都不难，主要是考察对代码的掌控能力 。也就是说，想法很简单，但实现起来可能就不是那么回事了。

首先要知道数组在内存中的存储方式，这样才能真正理解数组相关的面试题

数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

举一个字符数组的例子，如图所示：

需要两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以在删除或者增添元素的时候，就难免要移动其他元素的地址。

例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

而且大家如果使用C++的话，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。

• 数组的元素是不能删的，只能覆盖。

那么二维数组直接上图，大家应该就知道怎么回事了

那么二维数组在内存的空间地址是连续的么？

来举一个Java的例子，例如： int[][] rating = new int[3][4];， 这个二维数组在内存空间可不是一个 3*4 的连续地址空间

看了下图，就应该明白了：

此时的内存地址空间应该是一个对应行数的大小为3的连续内存地址空间，其每一个元素指向三条对应列数的大小为4的连续内存地址空间，所以Java的二维数组在内存中不是 3*4 的连续地址空间，而是四条连续的地址空间组成！

数组的经典题目

在面试中，数组是必考的基础数据结构。

其实数组的题目在思想上一般比较简单的，但是如果想高效，并不容易。

之前一共讲解了四道经典数组题目，每一道题目都代表一个类型，一种思想。

1. 二分法

• 704. 二分查找

这道题目考察数组的基本操作，可以使用暴力解法，通过这道题目，如果追求更优的算法，建议试一试用二分法，来解决这道题目

• 暴力解法时间复杂度：O(n)
• 二分法时间复杂度：O(logn)

在这道题目中讲到了循环不变量原则，只有在循环中坚持对区间的定义，才能清楚的把握循环中的各种细节。

二分法是算法面试中的常考题，建议通过这道题目，锻炼自己手撕二分的能力。

2. 双指针法

• 27. 移除元素

双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

• 暴力解法时间复杂度：O(n^2)
• 双指针时间复杂度：O(n)

这道题目迷惑了不少同学，纠结于数组中的元素为什么不能删除，主要是因为以下两点：

• 数组在内存中是连续的地址空间，不能释放单一元素，如果要释放，就是全释放（程序运行结束，回收内存栈空间）。
• C++中vector和array的区别一定要弄清楚，vector的底层实现是array，封装后使用更友好。

双指针法（快慢指针法）在数组和链表的操作中是非常常见的，很多考察数组和链表操作的面试题，都使用双指针法。

3. 滑动窗口

• 209.长度最小的子数组

本题介绍了数组操作中的另一个重要思想：滑动窗口。

• 暴力解法时间复杂度：O(n^2)
• 滑动窗口时间复杂度：O(n)

本题中，主要要理解滑动窗口如何移动 窗口起始位置，达到动态更新窗口大小的，从而得出长度最小的符合条件的长度。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。

如果没有接触过这一类的方法，很难想到类似的解题思路，滑动窗口方法还是很巧妙的。

4.模拟行为

• 59.螺旋矩阵II

在这道题目中，再一次介绍到了循环不变量原则，其实这也是写程序中的重要原则。

相信大家有遇到过这种情况： 感觉题目的边界调节超多，一波接着一波的判断，找边界，拆了东墙补西墙，好不容易运行通过了，代码写的十分冗余，毫无章法，其实真正解决题目的代码都是简洁的，或者有原则性的，大家可以在这道题目中体会到这一点。

总结导图