栈与队列

理论基础
队列是先进先出,栈是先进后出。如图所示:

栈和队列是STL(C++标准库)里面的两个数据结构。
C++标准库是有多个版本的,不同版本的STL,才能知道对应的栈和队列的实现原理。
那么来介绍一下,三个最普遍的STL版本:
-
HP STL
其他版本的C++ STL,一般是以HP STL为蓝本实现出来的,HP STL是C++ STL的第一个实现版本,而且开放源代码。 -
P.J.Plauger STL
由P.J.Plauger参照HP STL实现出来的,被Visual C++编译器所采用,不是开源的。 -
SGI STL
由Silicon Graphics Computer Systems公司参照HP STL实现,被Linux的C++编译器GCC所采用,SGI STL是开源软件,源码可读性甚高。
接下来介绍的栈和队列也是SGI STL里面的数据结构, 知道了使用版本,才知道对应的底层实现。
来说一说栈,栈先进后出,如图所示:
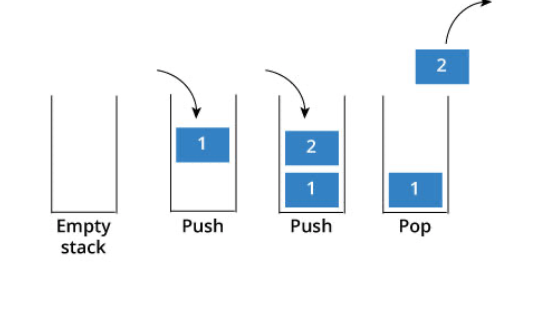
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也**不提供迭代器**(iterator)。 不像是set或者map提供迭代器iterator来遍历所有元素。
栈是以底层容器完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能)。
所以STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。
那么,STL中栈是用什么容器实现的?
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
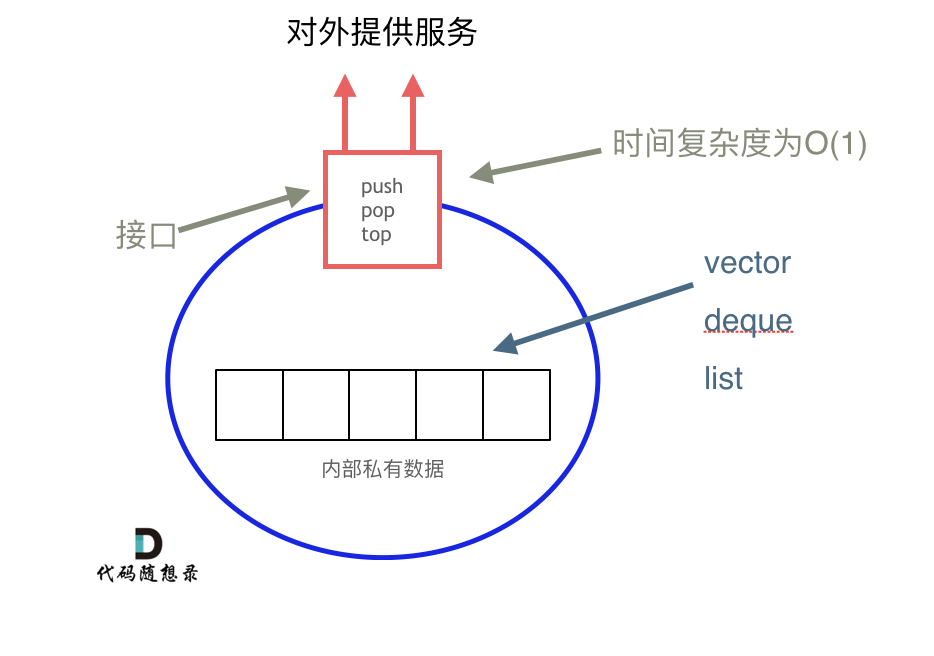
我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。
deque是一个双向队列,只要封住一段,只开通另一端就可以实现栈的逻辑了。
SGI STL中 队列底层实现缺省情况下一样使用deque实现的。
我们也可以指定vector为栈的底层实现,初始化语句如下:
1 | std::stack<int, std::vector<int> > third; // 使用vector为底层容器的栈 |
刚刚讲过栈的特性,对应的队列的情况是一样的。
队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。
也可以指定list 为起底层实现,初始化queue的语句如下:
1 | std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列 |
所以STL 队列也不被归类为容器,而被归类为container adapter( 容器适配器)。
我这里讲的都是C++ 语言中的情况, 使用其他语言的同学也要思考栈与队列的底层实现问题, 不要对数据结构的使用浅尝辄止,而要深挖其内部原理,才能夯实基础。
232.用栈实现队列
使用栈实现队列的下列操作:
push(x) – 将一个元素放入队列的尾部。
pop() – 从队列首部移除元素。
peek() – 返回队列首部的元素。
empty() – 返回队列是否为空。
示例:
1 | MyQueue queue = new MyQueue(); |
说明:
- 你只能使用标准的栈操作 – 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
- 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
- 假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)。
思路
这是一道模拟题,不涉及到具体算法,考察的就是对栈和队列的掌握程度。
使用栈来模拟队列的行为,如果仅仅用一个栈,是一定不行的,所以需要两个栈一个输入栈,一个输出栈,这里要注意输入栈和输出栈的关系。
下面动画模拟以下队列的执行过程:
执行语句:
queue.push(1);
queue.push(2);
queue.pop(); 注意此时的输出栈的操作
queue.push(3);
queue.push(4);
queue.pop();
queue.pop();注意此时的输出栈的操作
queue.pop();
queue.empty();

在push数据的时候,只要数据放进输入栈就好,但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入),再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了。
最后如何判断队列为空呢?如果进栈和出栈都为空的话,说明模拟的队列为空了。
在代码实现的时候,会发现pop() 和 peek()两个函数功能类似,代码实现上也是类似的,可以思考一下如何把代码抽象一下。
C++代码
- 时间复杂度: push和empty为
, pop和peek为 - 空间复杂度:
1 | class MyQueue { |
拓展
可以看出peek()的实现,直接复用了pop(), 要不然,对stOut判空的逻辑又要重写一遍。
再多说一些代码开发上的习惯问题,在工业级别代码开发中,最忌讳的就是 实现一个类似的函数,直接把代码粘过来改一改就完事了。
这样的项目代码会越来越乱,一定要懂得复用,功能相近的函数要抽象出来,不要大量的复制粘贴,很容易出问题!(踩过坑的人自然懂)
工作中如果发现某一个功能自己要经常用,同事们可能也会用到,自己就花点时间把这个功能抽象成一个好用的函数或者工具类,不仅自己方便,也方便了同事们。
225. 用队列实现栈
使用队列实现栈的下列操作:
- push(x) – 元素 x 入栈
- pop() – 移除栈顶元素
- top() – 获取栈顶元素
- empty() – 返回栈是否为空
注意:
- 你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
- 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
- 你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
思路
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时再去弹出元素就是栈的顺序了。
C++代码
1 | class MyStack { |
- 时间复杂度: push为O(n),其他为O(1)
- 空间复杂度: O(n)
20. 有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 注意空字符串可被认为是有效字符串。
示例 1:
- 输入: “()”
- 输出: true
示例 2:
- 输入: “()[]{}”
- 输出: true
示例 3:
- 输入: “(]”
- 输出: false
示例 4:
- 输入: “([)]”
- 输出: false
示例 5:
- 输入: “{[]}”
- 输出: true
思路
**括号匹配是使用栈解决的经典问题。**在编译原理中,编译器在词法分析的过程中处理括号、花括号等这个符号的逻辑,也是使用了栈这种数据结构。在linux系统中,cd这个进入目录的命令,cd a/b/c/../../,这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用(其实可以出一道相应的面试题了)。
由于栈结构的特殊性,非常适合做对称匹配类的题目。首先要弄清楚,字符串里的括号不匹配有几种情况。
- 第一种情况,字符串里左方向的括号多余
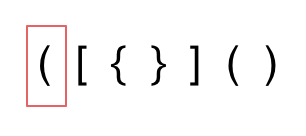
- 第二种情况,括号没有多余,但是括号的类型没有匹配上。
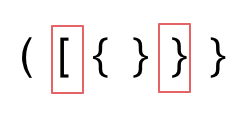
- 第三种情况,字符串里右方向的括号多余了,所以不匹配。
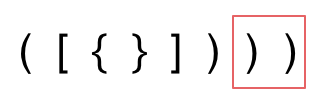
我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。

第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
分析完之后,代码其实就比较好写了,
但还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
C++代码
- 时间复杂度:
- 空间复杂度:
1 | class Solution { |
1047. 删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
- 输入:“abbaca”
- 输出:“ca”
- 解释:例如,在 “abbaca” 中,我们可以删除 “bb” 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”,其中又只有 “aa” 可以执行重复项删除操作,所以最后的字符串为 “ca”。
提示:
- 1 <= S.length <= 20000
- S 仅由小写英文字母组成。
思路

C++代码
- 时间复杂度:
- 空间复杂度:
1 | class Solution { |
题外话
这道题目就像是我们玩过的游戏对对碰,如果相同的元素挨在一起就要消除。
可能我们在玩游戏的时候感觉理所当然应该消除,但程序又怎么知道该如何消除呢,特别是消除之后又有新的元素可能挨在一起。
此时游戏的后端逻辑就可以用一个栈来实现(我没有实际考察对对碰或者爱消除游戏的代码实现,仅从原理上进行推断)。
游戏开发可能使用栈结构,编程语言的一些功能实现也会使用栈结构,实现函数递归调用就需要栈,但不是每种编程语言都支持递归,例如:
递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
相信大家应该遇到过一种错误就是栈溢出,系统输出的异常是Segmentation fault(当然不是所有的Segmentation fault 都是栈溢出导致的) ,如果你使用了递归,就要想一想是不是无限递归了,那么系统调用栈就会溢出。
而且在企业项目开发中,尽量不要使用递归!在项目比较大的时候,由于参数多,全局变量等等,使用递归很容易判断不充分return的条件,非常容易无限递归(或者递归层级过深),造成栈溢出错误(这种问题还不好排查!)
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 + , - , * , / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
- 输入: [“2”, “1”, “+”, “3”, " * "]
- 输出: 9
- 解释: 该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
- 输入: [“4”, “13”, “5”, “/”, “+”]
- 输出: 6
- 解释: 该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
-
输入: [“10”, “6”, “9”, “3”, “+”, “-11”, " * ", “/”, " * ", “17”, “+”, “5”, “+”]
-
输出: 22
-
解释:该算式转化为常见的中缀算术表达式为:
1
2
3
4
5
6
7((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
逆波兰表达式:是一种后缀表达式,所谓后缀就是指运算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
-
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
-
适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈中。
思路

C++代码
- 时间复杂度:
- 空间复杂度:
1 | class Solution { |
题外话
我们习惯看到的表达式都是中缀表达式,因为符合我们的习惯,但是中缀表达式对于计算机就很不友好了。
例如:4 + 13 / 5,这就是中缀表达式,计算机从左到右去扫描的话,扫到13,还要判断13后面是什么运算符,还要比较一下优先级,然后13还和后面的5做运算,做完运算之后,还要向前回退到 4 的位置,继续做加法,你说麻不麻烦!
那么将中缀表达式,转化为后缀表达式之后:[“4”, “13”, “5”, “/”, “+”] ,就不一样了,计算机可以利用栈来顺序处理,不需要考虑优先级了。也不用回退了, 所以后缀表达式对计算机来说是非常友好的。
可以说本题不仅仅是一道好题,也展现出计算机的思考方式。
在1970年代和1980年代,惠普在其所有台式和手持式计算器中都使用了RPN(后缀表达式),直到2020年代仍在某些模型中使用了RPN。
239. 滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?

思路
这是使用单调队列的经典题目。
我们需要一个队列,这个队列放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
1 | class MyQueue { |
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。
维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列。
设计单调队列的时候,pop和push操作要保持如下规则:
pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:

使用deque的数据结构最为合适,在文章栈与队列:来看看栈和队列不为人知的一面中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
扩展
首先要明确的是,题解中单调队列里的pop和push接口,仅适用于本题。单调队列不是一成不变的,而是不同场景不同写法,总之要保证队列里单调递减或递增的原则,所以叫做单调队列。 不要以为本题中的单调队列实现就是固定的写法。
C++中deque是stack和queue默认的底层实现容器(这个我们之前已经讲过啦),deque是可以两边扩展的,而且deque里元素并不是严格的连续分布的。
C++代码
- 时间复杂度:
- 空间复杂度:
1 | class Solution { |
347.前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素。
示例 1:
- 输入: nums = [1,1,1,2,2,3], k = 2
- 输出: [1,2]
示例 2:
- 输入: nums = [1], k = 1
- 输出: [1]
提示:
- 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
- 你的算法的时间复杂度必须优于
, n 是数组的大小。 - 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
- 你可以按任意顺序返回答案。
思路
这道题目主要涉及到如下三块内容:
- 要统计元素出现频率
- 对频率排序
- 找出前K个高频元素
首先. 统计元素出现的频率,这一类的问题可以使用map来进行统计。然后对频率进行排序,这里可以使用一种容器适配器就是优先级队列。
优先级队列其实就是一个披着队列外衣的堆,因为优先级队列对外接口只是从队头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列。
而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢?
缺省情况下priority_queue利用max-heap(大顶堆)完成对元素的排序,这个大顶堆是以vector为表现形式的complete binary tree(完全二叉树)。
堆是一棵完全二叉树,树中每个结点的值都不小于(或不大于)其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆,小于等于左右孩子就是小顶堆。
所以大家经常说的大顶堆(堆头是最大元素),小顶堆(堆头是最小元素),如果懒得自己实现的话,就直接用priority_queue(优先级队列)就可以了,底层实现都是一样的,从小到大排就是小顶堆,从大到小排就是大顶堆。
本题我们就要使用优先级队列来对部分频率进行排序。
为什么不用快排呢, 使用快排要将map转换为vector的结构,然后对整个数组进行排序, 而这种场景下,我们其实只需要维护k个有序的序列就可以了,所以使用优先级队列是最优的。
此时要思考一下,是使用小顶堆呢,还是大顶堆?
有的同学一想,题目要求前 K 个高频元素,那么果断用大顶堆啊。
那么问题来了,定义一个大小为k的大顶堆,在每次移动更新大顶堆的时候,每次弹出都把最大的元素弹出去了,那么怎么保留下来前K个高频元素呢。
而且使用大顶堆就要把所有元素都进行排序,那能不能只排序k个元素呢?
所以我们要用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。
寻找前k个最大元素流程如图所示:(图中的频率只有三个,所以正好构成一个大小为3的小顶堆,如果频率更多一些,则用这个小顶堆进行扫描)

C++代码
1 | class Solution { |
拓展
大家对这个比较运算在建堆时是如何应用的,为什么左大于右就会建立小顶堆,反而建立大顶堆比较困惑。
确实 例如我们在写快排的cmp函数的时候,return left>right 就是从大到小,return left<right 就是从小到大。
优先级队列的定义正好反过来了,可能和优先级队列的源码实现有关(我没有仔细研究),我估计是底层实现上优先队列队首指向后面,队尾指向最前面的缘故!
总结
栈与队列的理论基础
首先我们在栈与队列:来看看栈和队列不为人知的一面中讲解了栈和队列的理论基础。
里面提到了灵魂四问:
- C++中stack,queue 是容器么?
- 我们使用的stack,queue是属于那个版本的STL?
- 我们使用的STL中stack,queue是如何实现的?
- stack,queue 提供迭代器来遍历空间么?
相信不仅仅是C++中有这些问题,那么大家使用其他编程语言,也可以考虑一下这四个问题,栈和队列是如何实现的。
栈与队列是我们熟悉的不能再熟悉的数据结构,但它们的底层实现,很多同学都比较模糊,这其实就是基础所在。
可以出一道面试题:栈里面的元素在内存中是连续分布的么?
这个问题有两个陷阱:
- 陷阱1:栈是容器适配器,底层容器使用不同的容器,导致栈内数据在内存中是不是连续分布。
- 陷阱2:缺省情况下,默认底层容器是deque,那么deque的在内存中的数据分布是什么样的呢? 答案是:不连续的,下文也会提到deque。
所以这就是考察候选者基础知识扎不扎实的好问题。
大家还是要多多重视起来!
了解了栈与队列基础之后,那么可以用栈与队列:栈实现队列 和 栈与队列:队列实现栈 来练习一下栈与队列的基本操作。
值得一提的是,用栈与队列:用队列实现栈还有点别扭中,其实只用一个队列就够了。
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时在去弹出元素就是栈的顺序了。
栈经典题目
栈在系统中的应用
如果还记得编译原理的话,编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑,就是使用了栈这种数据结构。
再举个例子,linux系统中,cd这个进入目录的命令我们应该再熟悉不过了。
1 | cd a/b/c/../../ |
这个命令最后进入a目录,系统是如何知道进入了a目录呢 ,这就是栈的应用。这在leetcode上也是一道题目,编号:71. 简化路径,大家有空可以做一下。
递归的实现是栈:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
所以栈在计算机领域中应用是非常广泛的。
有的同学经常会想学的这些数据结构有什么用,也开发不了什么软件,大多数同学说的软件应该都是可视化的软件例如APP、网站之类的,那都是非常上层的应用了,底层很多功能的实现都是基础的数据结构和算法。
所以数据结构与算法的应用往往隐藏在我们看不到的地方!
括号匹配问题
在栈与队列:系统中处处都是栈的应用中我们讲解了括号匹配问题。
括号匹配是使用栈解决的经典问题。
建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
先来分析一下 这里有三种不匹配的情况,
- 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
- 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
- 第三种情况,字符串里右方向的括号多余了,所以不匹配。
这里还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
字符串去重问题
在栈与队列:匹配问题都是栈的强项中讲解了字符串去重问题。1047. 删除字符串中的所有相邻重复项
思路就是可以把字符串顺序放到一个栈中,然后如果相同的话 栈就弹出,这样最后栈里剩下的元素都是相邻不相同的元素了。
逆波兰表达式问题
在栈与队列:有没有想过计算机是如何处理表达式的?中讲解了求逆波兰表达式。
本题中每一个子表达式要得出一个结果,然后拿这个结果再进行运算,那么这岂不就是一个相邻字符串消除的过程,和栈与队列:匹配问题都是栈的强项中的对对碰游戏是不是就非常像了。
队列的经典题目
滑动窗口最大值问题
在栈与队列:滑动窗口里求最大值引出一个重要数据结构中讲解了一种数据结构:单调队列。
这道题目还是比较绕的,如果第一次遇到这种题目,需要反复琢磨琢磨
主要思想是队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。
那么这个维护元素单调递减的队列就叫做单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来一个单调队列
而且不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。
设计单调队列的时候,pop,和push操作要保持如下规则:
- pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
- push(value):如果push的元素value大于入口元素的数值,那么就将队列出口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
一些同学还会对单调队列都有一些困惑,首先要明确的是,题解中单调队列里的pop和push接口,仅适用于本题。
单调队列不是一成不变的,而是不同场景不同写法,总之要保证队列里单调递减或递增的原则,所以叫做单调队列。
不要以为本地中的单调队列实现就是固定的写法。
我们用deque作为单调队列的底层数据结构,C++中deque是stack和queue默认的底层实现容器(这个我们之前已经讲过),deque是可以两边扩展的,而且deque里元素并不是严格的连续分布的。
求前 K 个高频元素
在栈与队列:求前 K 个高频元素和队列有啥关系?中讲解了求前 K 个高频元素。
通过求前 K 个高频元素,引出另一种队列就是优先级队列。
什么是优先级队列呢?
其实就是一个披着队列外衣的堆,因为优先级队列对外接口只是从队头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列。
而且优先级队列内部元素是自动依照元素的权值排列。那么它是如何有序排列的呢?
缺省情况下priority_queue利用max-heap(大顶堆)完成对元素的排序,这个大顶堆是以vector为表现形式的complete binary tree(完全二叉树)。
什么是堆呢?
堆是一棵完全二叉树,树中每个结点的值都不小于(或不大于)其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆,小于等于左右孩子就是小顶堆。
所以大家经常说的大顶堆(堆头是最大元素),小顶堆(堆头是最小元素),如果懒得自己实现的话,就直接用priority_queue(优先级队列)就可以了,底层实现都是一样的,从小到大排就是小顶堆,从大到小排就是大顶堆。
本题就要使用优先级队列来对部分频率进行排序。 注意这里是对部分数据进行排序而不需要对所有数据排序!
所以排序的过程的时间复杂度是
总结
在栈与队列系列中,我们强调栈与队列的基础,也是很多同学容易忽视的点。
使用抽象程度越高的语言,越容易忽视其底层实现,而C++相对来说是比较接近底层的语言。
我们用栈实现队列,用队列实现栈来掌握的栈与队列的基本操作。
接着,通过括号匹配问题、字符串去重问题、逆波兰表达式问题来系统讲解了栈在系统中的应用,以及使用技巧。
通过求滑动窗口最大值,以及前K个高频元素介绍了两种队列:单调队列和优先级队列,这是特殊场景解决问题的利器,是一定要掌握的。
好了,栈与队列我们就总结到这里了,接下来Carl就要带大家开启新的篇章了,大家加油!œ
预览: