二叉树的修改与构造

Channing Hsu
  2023-08-28 09:20:17 2023-08-28 09:20:17 创建   2024-12-03 01:50:49 2024-12-03 01:50:49 更新      5.9k 字  24 分钟  

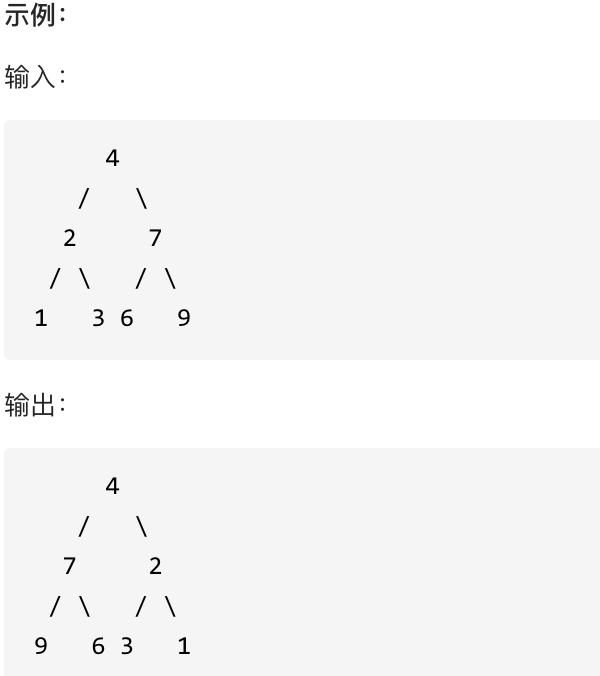
226.翻转二叉树

力扣题目链接

翻转一棵二叉树。

226.翻转二叉树

这道题目背后有一个让程序员心酸的故事，听说 Homebrew的作者Max Howell，就是因为没在白板上写出翻转二叉树，最后被Google拒绝了。

思路

我们之前介绍的都是各种方式遍历二叉树，这次要翻转了，感觉还是有点懵逼。

这得怎么翻转呢？

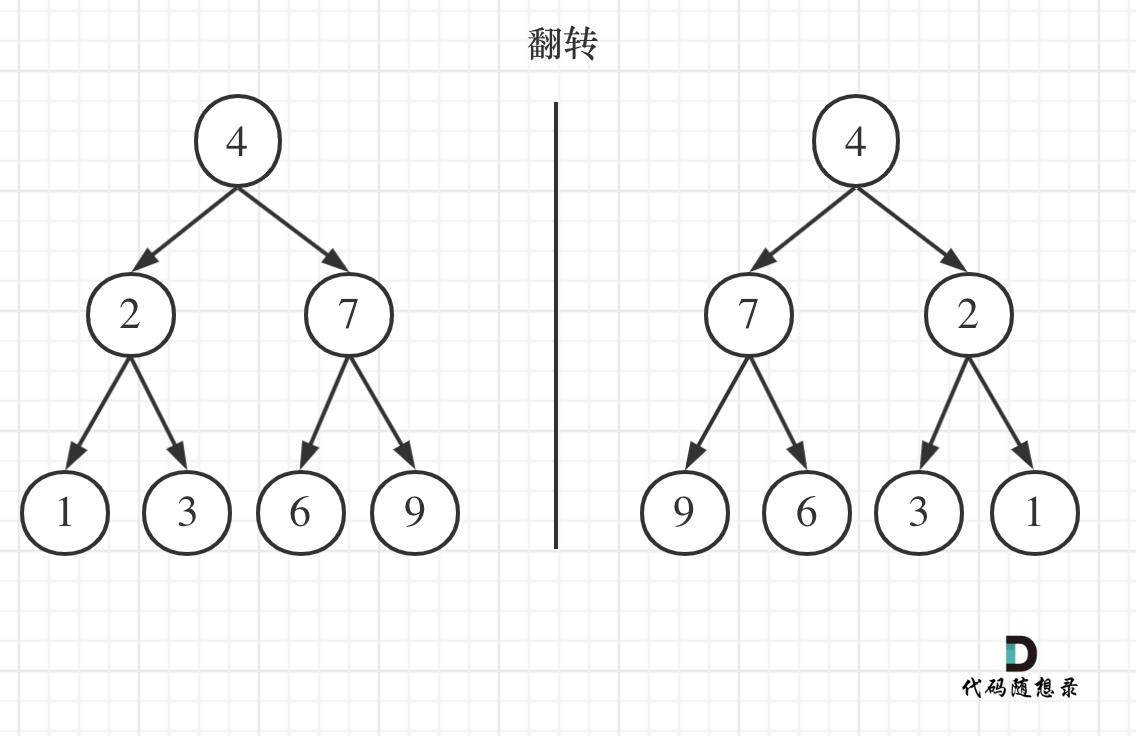
如果要从整个树来看，翻转还真的挺复杂，整个树以中间分割线进行翻转，如图：

226.翻转二叉树1

可以发现想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。

关键在于遍历顺序，前中后序应该选哪一种遍历顺序？ （一些同学这道题都过了，但是不知道自己用的是什么顺序）

遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。

注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果

这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！建议拿纸画一画，就理解了

那么层序遍历可以不可以呢？依然可以的！只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的！

递归法

对于二叉树的递归法的前中后序遍历，已经在二叉树：前中后序递归遍历详细讲解了。

我们下文以前序遍历为例，通过动画来看一下翻转的过程:

翻转二叉树

我们来看一下递归三部曲：

  1. 确定递归函数的参数和返回值

参数就是要传入节点的指针，不需要其他参数了，通常此时定下来主要参数，如果在写递归的逻辑中发现还需要其他参数的时候，随时补充。

返回值的话其实也不需要，但是题目中给出的要返回root节点的指针，可以直接使用题目定义好的函数，所以就函数的返回类型为TreeNode*。

1
TreeNode* invertTree(TreeNode* root)
  1. 确定终止条件

当前节点为空的时候，就返回

1
if (root == NULL) return root;
  1. 确定单层递归的逻辑

因为是先前序遍历，所以先进行交换左右孩子节点，然后反转左子树，反转右子树。

1
2
3
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);

基于这递归三步法，代码基本写完，C++代码如下：

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 左
        invertTree(root->right);        // 右
        return root;
    }
};

迭代法

深度优先遍历

二叉树：听说递归能做的，栈也能做！中给出了前中后序迭代方式的写法，所以本题可以很轻松的写出如下迭代法的代码：

C++代码迭代法（前序遍历）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()) {
            TreeNode* node = st.top();              // 中
            st.pop();
            swap(node->left, node->right);
            if(node->right) st.push(node->right);   // 右
            if(node->left) st.push(node->left);     // 左
        }
        return root;
    }
};

如果这个代码看不懂的话可以再回顾一下二叉树：听说递归能做的，栈也能做！。

我们在二叉树：前中后序迭代方式的统一写法中介绍了统一的写法，所以，本题也只需将文中的代码少做修改便可。

C++代码如下迭代法（前序遍历）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);                          // 中
                st.push(NULL);
            } else {
                st.pop();
                node = st.top();
                st.pop();
                swap(node->left, node->right);          // 节点处理逻辑
            }
        }
        return root;
    }
};

如果上面这个代码看不懂，回顾一下文章二叉树：前中后序迭代方式的统一写法。

广度优先遍历

也就是层序遍历，层数遍历也是可以翻转这棵树的，因为层序遍历也可以把每个节点的左右孩子都翻转一遍，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                swap(node->left, node->right); // 节点处理
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }
};

如果对以上代码不理解，或者不清楚二叉树的层序遍历，可以看这篇二叉树：层序遍历登场！

106.从中序与后序遍历序列构造二叉树

力扣题目链接

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

  • 中序遍历 inorder = [9,3,15,20,7]
  • 后序遍历 postorder = [9,15,7,20,3]
    返回如下的二叉树：

思路

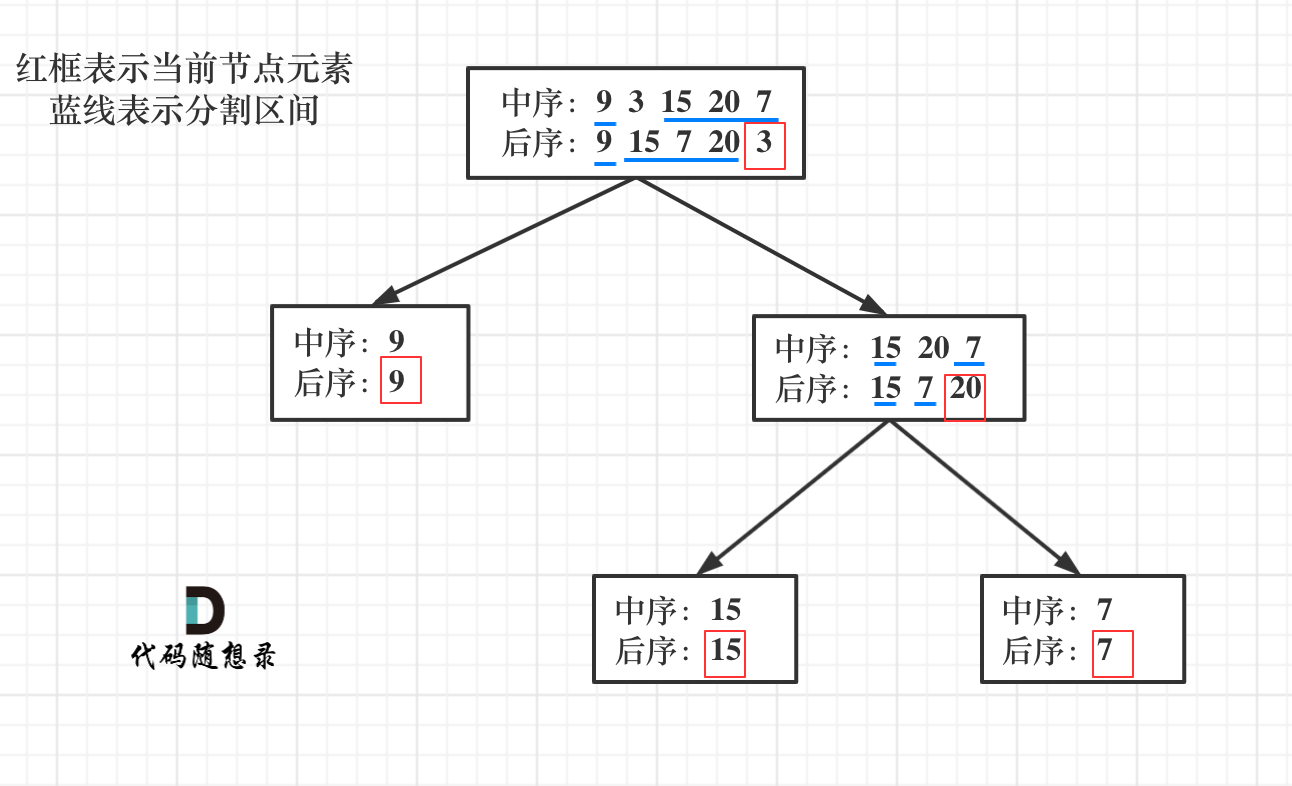
首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

如果让我们肉眼看两个序列，画一棵二叉树的话，应该分分钟都可以画出来。

流程如图：

106.从中序与后序遍历序列构造二叉树

那么代码应该怎么写呢？

说到一层一层切割，就应该想到了递归。

说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

  • 第一步：如果数组大小为零的话，说明是空节点了。

  • 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

  • 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

  • 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

  • 第五步：切割后序数组，切成后序左数组和后序右数组

  • 第六步：递归处理左区间和右区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
private:
    TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
        if (postorder.size() == 0) return NULL;

        // 后序遍历数组最后一个元素，就是当前的中间节点
        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);

        // 叶子节点
        if (postorder.size() == 1) return root;

        // 找到中序遍历的切割点
        int delimiterIndex;
        for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }

        // 切割中序数组
        // 左闭右开区间：[0, delimiterIndex)
        vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
        // [delimiterIndex + 1, end)
        vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );

        // postorder 舍弃末尾元素
        postorder.resize(postorder.size() - 1);

        // 切割后序数组
        // 依然左闭右开，注意这里使用了左中序数组大小作为切割点
        // [0, leftInorder.size)
        vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
        // [leftInorder.size(), end)
        vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());

        root->left = traversal(leftInorder, leftPostorder);
        root->right = traversal(rightInorder, rightPostorder);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

下面给出用下标索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下标索引来分割）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
private:
    // 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)
    TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
        if (postorderBegin == postorderEnd) return NULL;

        int rootValue = postorder[postorderEnd - 1];
        TreeNode* root = new TreeNode(rootValue);

        if (postorderEnd - postorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组
        // 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)
        int leftPostorderBegin =  postorderBegin;
        int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
        // 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)
        int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
        int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        // 左闭右开的原则
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

105.从前序与中序遍历序列构造二叉树

力扣题目链接

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

105. 从前序与中序遍历序列构造二叉树

思路

本题和106是一样的道理。

带日志的版本C++代码如下： （带日志的版本仅用于调试，不要在leetcode上提交，会超时）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        cout << "----------" << endl;
        cout << "leftInorder :";
        for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
            cout << inorder[i] << " ";
        }
        cout << endl;

        cout << "rightInorder :";
        for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
            cout << inorder[i] << " ";
        }
        cout << endl;

        cout << "leftPreorder :";
        for (int i = leftPreorderBegin; i < leftPreorderEnd; i++) {
            cout << preorder[i] << " ";
        }
        cout << endl;

        cout << "rightPreorder :";
        for (int i = rightPreorderBegin; i < rightPreorderEnd; i++) {
            cout << preorder[i] << " ";
        }
        cout << endl;


        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());

    }
};

105.从前序与中序遍历序列构造二叉树，最后版本，C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;

        // 参数坚持左闭右开的原则
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

总结

之前我们讲的二叉树题目都是各种遍历二叉树，这次开始构造二叉树了，思路其实比较简单，但是真正代码实现出来并不容易。

所以要避免眼高手低，踏实地把代码写出来。

我同时给出了添加日志的代码版本，因为这种题目是不太容易写出来调一调就能过的，所以一定要把流程日志打出来，看看符不符合自己的思路。

大家遇到这种题目的时候，也要学会打日志来调试（如何打日志有时候也是个技术活），不要脑动模拟，脑动模拟很容易越想越乱。

最后我还给出了为什么前序和中序可以唯一确定一棵二叉树，后序和中序可以唯一确定一棵二叉树，而前序和后序却不行。

认真研究完本篇，相信大家对二叉树的构造会清晰很多。

654.最大二叉树

力扣题目地址

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

  • 二叉树的根是数组中的最大元素。
  • 左子树是通过数组中最大值左边部分构造出的最大二叉树。
  • 右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例 ：

654.最大二叉树

提示：

给定的数组的大小在 [1, 1000] 之间。

思路

最大二叉树的构建过程如下：

654.最大二叉树

构造树一般采用的是前序遍历，因为先构造中间节点，然后递归构造左子树和右子树。

  • 确定递归函数的参数和返回值

参数传入的是存放元素的数组，返回该数组构造的二叉树的头结点，返回类型是指向节点的指针。

代码如下：

1
2
TreeNode* constructMaximumBinaryTree(vector<int>& nums)

  • 确定终止条件

题目中说了输入的数组大小一定是大于等于1的，所以我们不用考虑小于1的情况，那么当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点了。

那么应该定义一个新的节点，并把这个数组的数值赋给新的节点，然后返回这个节点。 这表示一个数组大小是1的时候，构造了一个新的节点，并返回。

代码如下：

1
2
3
4
5
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
    node->val = nums[0];
    return node;
}
  • 确定单层递归的逻辑

这里有三步工作

  1. 先要找到数组中最大的值和对应的下标， 最大的值构造根节点，下标用来下一步分割数组。

代码如下：

1
2
3
4
5
6
7
8
9
10
int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {
    if (nums[i] > maxValue) {
        maxValue = nums[i];
        maxValueIndex = i;
    }
}
TreeNode* node = new TreeNode(0);
node->val = maxValue;
  1. 最大值所在的下标左区间 构造左子树

这里要判断maxValueIndex > 0，因为要保证左区间至少有一个数值。

代码如下：

1
2
3
4
if (maxValueIndex > 0) {
    vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
    node->left = constructMaximumBinaryTree(newVec);
}
  1. 最大值所在的下标右区间 构造右子树

判断maxValueIndex < (nums.size() - 1)，确保右区间至少有一个数值。

代码如下：

1
2
3
4
if (maxValueIndex < (nums.size() - 1)) {
    vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
    node->right = constructMaximumBinaryTree(newVec);
}

这样我们就分析完了，整体代码如下：（详细注释）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        TreeNode* node = new TreeNode(0);
        if (nums.size() == 1) {
            node->val = nums[0];
            return node;
        }
        // 找到数组中最大的值和对应的下标
        int maxValue = 0;
        int maxValueIndex = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] > maxValue) {
                maxValue = nums[i];
                maxValueIndex = i;
            }
        }
        node->val = maxValue;
        // 最大值所在的下标左区间 构造左子树
        if (maxValueIndex > 0) {
            vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
            node->left = constructMaximumBinaryTree(newVec);
        }
        // 最大值所在的下标右区间 构造右子树
        if (maxValueIndex < (nums.size() - 1)) {
            vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
            node->right = constructMaximumBinaryTree(newVec);
        }
        return node;
    }
};

以上代码比较冗余，效率也不高，每次还要切割的时候每次都要定义新的vector（也就是数组），但逻辑比较清晰。

和文章二叉树：构造二叉树登场！中一样的优化思路，就是每次分隔不用定义新的数组，而是通过下标索引直接在原数组上操作。

优化后代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
private:
    // 在左闭右开区间[left, right)，构造二叉树
    TreeNode* traversal(vector<int>& nums, int left, int right) {
        if (left >= right) return nullptr;

        // 分割点下标：maxValueIndex
        int maxValueIndex = left;
        for (int i = left + 1; i < right; ++i) {
            if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
        }

        TreeNode* root = new TreeNode(nums[maxValueIndex]);

        // 左闭右开：[left, maxValueIndex)
        root->left = traversal(nums, left, maxValueIndex);

        // 左闭右开：[maxValueIndex + 1, right)
        root->right = traversal(nums, maxValueIndex + 1, right);

        return root;
    }
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traversal(nums, 0, nums.size());
    }
};

拓展

可以发现上面的代码看上去简洁一些，主要是因为第二版其实是允许空节点进入递归，所以不用在递归的时候加判断节点是否为空

第一版递归过程：（加了if判断，为了不让空节点进入递归）

1
2
3
4
5
6
7
8
9
if (maxValueIndex > 0) { // 这里加了判断是为了不让空节点进入递归
    vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
    node->left = constructMaximumBinaryTree(newVec);
}

if (maxValueIndex < (nums.size() - 1)) { // 这里加了判断是为了不让空节点进入递归
    vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
    node->right = constructMaximumBinaryTree(newVec);
}

第二版递归过程： （如下代码就没有加if判断）

1
2
3
root->left = traversal(nums, left, maxValueIndex);

root->right = traversal(nums, maxValueIndex + 1, right);

第二版代码是允许空节点进入递归，所以没有加if判断，当然终止条件也要有相应的改变。

第一版终止条件，是遇到叶子节点就终止，因为空节点不会进入递归。

第二版相应的终止条件，是遇到空节点，也就是数组区间为0，就终止了。

总结

这道题目其实和 二叉树：构造二叉树登场！ 是一个思路，比二叉树：构造二叉树登场！ 还简单一些。

注意类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下标索引直接在原数组上操作，这样可以节约时间和空间上的开销。

一些同学也会疑惑，什么时候递归函数前面加if，什么时候不加if，这个问题我在最后也给出了解释。

其实就是不同代码风格的实现，一般情况来说：如果让空节点（空指针）进入递归，就不加if，如果不让空节点进入递归，就加if限制一下， 终止条件也会相应的调整。

617.合并二叉树

力扣题目链接

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

617.合并二叉树

注意: 合并必须从两个树的根节点开始。

思路

相信这道题目很多同学疑惑的点是如何同时遍历两个二叉树呢？

其实和遍历一个树逻辑是一样的，只不过传入两个树的节点，同时操作。

递归

二叉树使用递归，就要想使用前中后哪种遍历方式？

本题使用哪种遍历都是可以的！

我们下面以前序遍历为例。

动画如下：

617.合并二叉树

那么我们来按照递归三部曲来解决：

  1. 确定递归函数的参数和返回值：

首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。

代码如下：

1
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
  1. 确定终止条件：

因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了（如果t2也为NULL也无所谓，合并之后就是NULL）。

反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。

代码如下：

1
2
if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1
  1. 确定单层递归的逻辑：

单层递归的逻辑就比较好写了，这里我们重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。

那么单层递归中，就要把两棵树的元素加到一起。

1
t1->val += t2->val;

接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。

t1 的右子树：是 合并 t1右子树 t2右子树之后的右子树。

最终t1就是合并之后的根节点。

代码如下：

1
2
3
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;

此时前序遍历，完整代码就写出来了，如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
        if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1
        // 修改了t1的数值和结构
        t1->val += t2->val;                             // 中
        t1->left = mergeTrees(t1->left, t2->left);      // 左
        t1->right = mergeTrees(t1->right, t2->right);   // 右
        return t1;
    }
};

那么中序遍历也是可以的，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
        if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1
        // 修改了t1的数值和结构
        t1->left = mergeTrees(t1->left, t2->left);      // 左
        t1->val += t2->val;                             // 中
        t1->right = mergeTrees(t1->right, t2->right);   // 右
        return t1;
    }
};

后序遍历依然可以，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
        if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1
        // 修改了t1的数值和结构
        t1->left = mergeTrees(t1->left, t2->left);      // 左
        t1->right = mergeTrees(t1->right, t2->right);   // 右
        t1->val += t2->val;                             // 中
        return t1;
    }
};

但是前序遍历是最好理解的，我建议大家用前序遍历来做就OK。

如上的方法修改了t1的结构，当然也可以不修改t1和t2的结构，重新定义一个树。

不修改输入树的结构，前序遍历，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if (t1 == NULL) return t2;
        if (t2 == NULL) return t1;
        // 重新定义新的节点，不修改原有两个树的结构
        TreeNode* root = new TreeNode(0);
        root->val = t1->val + t2->val;
        root->left = mergeTrees(t1->left, t2->left);
        root->right = mergeTrees(t1->right, t2->right);
        return root;
    }
};

总结

合并二叉树，也是二叉树操作的经典题目，如果没有接触过的话，其实并不简单，因为我们习惯了操作一个二叉树，一起操作两个二叉树，还会有点懵懵的。

这不是我们第一次操作两棵二叉树了，在二叉树：我对称么？中也一起操作了两棵二叉树。

评论
目录
二叉树的修改与构造
  1. 226.翻转二叉树
    1. 思路
  2. 106.从中序与后序遍历序列构造二叉树
    1. 思路
  3. 105.从前序与中序遍历序列构造二叉树
    1. 思路
    2. 总结
  4. 654.最大二叉树
    1. 思路
    2. 拓展
    3. 总结
  5. 617.合并二叉树
    1. 思路
    2. 总结