动态规划 8️⃣

300.最长递增子序列

力扣题目链接

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

1 <= nums.length <= 2500
-10^4 <= nums[i] <= 104

思路

首先通过本题大家要明确什么是子序列，“子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序”。

本题也是代码随想录中子序列问题的第一题，如果没接触过这种题目的话，本题还是很难的，甚至想暴力去搜索也不知道怎么搜。
子序列问题是动态规划解决的经典问题，当前下标i的递增子序列长度，其实和i之前的下标j的子序列长度有关系，那又是什么样的关系呢。

接下来，依然用动规五部曲来详细分析一波：

dp[i]的定义

本题中，正确定义dp数组的含义十分重要。

dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度

为什么一定表示 “以nums[i]结尾的最长递增子序” ，因为做递增比较的时候，如果比较 nums[j] 和 nums[i] 的大小，那么两个递增子序列一定分别以nums[j]为结尾和 nums[i]为结尾，要不然这个比较就没有意义了，不是尾部元素的比较那么如何算递增呢。

状态转移方程

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

所以：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

注意这里不是要dp[i] 与 dp[j] + 1进行比较，而是要取dp[j] + 1的最大值。

dp[i]的初始化

每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1.

确定遍历顺序

dp[i] 是有0到i-1各个位置的最长递增子序列推导而来，那么遍历i一定是从前向后遍历。

j其实就是遍历0到i-1，那么是从前到后，还是从后到前遍历都无所谓，只要吧 0 到 i-1 的元素都遍历了就行了。所以默认习惯从前向后遍历。

遍历i的循环在外层，遍历j则在内层，代码如下：

for (int i = 1; i < nums.size(); i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
    }
    if (dp[i] > result) result = dp[i]; // 取长的子序列
}

举例推导dp数组

输入：[0,1,0,3,2]，dp数组的变化如下：

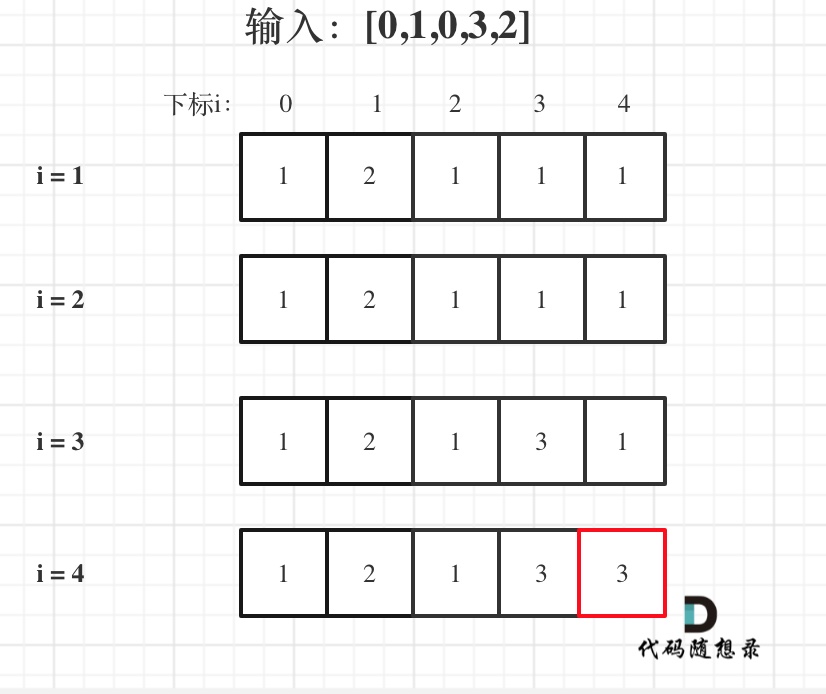
如果代码写出来，但一直AC不了，那么就把dp数组打印出来，看看对不对！

以上五部分析完毕，C++代码如下：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) result = dp[i]; // 取长的子序列
        }
        return result;
    }
};

时间复杂度:
空间复杂度:

总结

本题最关键的是要想到dp[i]由哪些状态可以推出来，并取最大值，那么很自然就能想到递推公式：dp[i] = max(dp[i], dp[j] + 1);

674. 最长连续递增序列

力扣题目链接

给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

连续递增的子序列可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

0 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

动态规划

动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i]：以下标i为结尾的连续递增的子序列长度为dp[i]。

注意这里的定义，一定是以下标i为结尾，并不是说一定以下标0为起始位置。

确定递推公式

如果 nums[i] > nums[i - 1]，那么以 i 为结尾的连续递增的子序列长度一定等于以i - 1为结尾的连续递增的子序列长度 + 1 。

即：dp[i] = dp[i - 1] + 1;

因为本题要求连续递增子序列，所以就只要比较nums[i]与nums[i - 1]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。

既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i] 和 nums[i - 1]。

这里大家要好好体会一下！

dp数组如何初始化

以下标i为结尾的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。

所以dp[i]应该初始1;

确定遍历顺序

从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。

本文在确定递推公式的时候也说明了为什么本题只需要一层for循环，代码如下：

举例推导dp数组

已输入nums = [1,3,5,4,7]为例，dp数组状态如下：

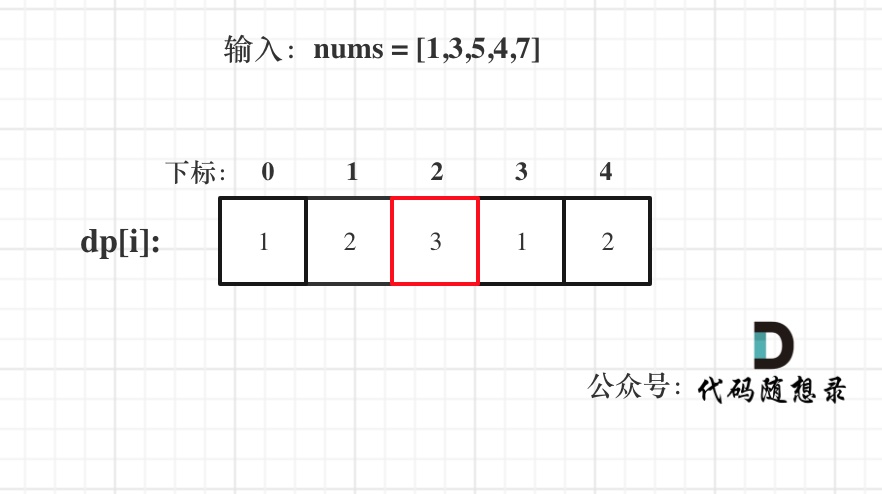
注意这里要取dp[i]里的最大值，所以dp[2]才是结果！

以上分析完毕，C++代码如下：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int result = 1;
        vector<int> dp(nums.size() ,1);
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

贪心

这道题目也可以用贪心来做，也就是遇到nums[i] > nums[i - 1]的情况，count就++，否则count为1，记录count的最大值就可以了。

代码如下：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        int result = 1; // 连续子序列最少也是1
        int count = 1;
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                count++;
            } else { // 不连续，count从头开始
                count = 1;
            }
            if (count > result) result = count;
        }
        return result;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

总结

本题也是动规里子序列问题的经典题目，但也可以用贪心来做，大家也会发现贪心好像更简单一点，而且空间复杂度仅是O(1)。

要联动起来，才能理解递增子序列怎么求，递增连续子序列又要怎么求。

概括来说：不连续递增子序列的跟前0-i个状态有关，连续递增的子序列只跟前一个状态有关

718. 最长重复子数组

力扣题目链接

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

示例：

输入：

A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3, 2, 1] 。

提示：

1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100

思路

注意题目中说的子数组，其实就是连续子序列。

要求两个数组中最长重复子数组，如果是暴力的解法只需要先两层for循环确定两个数组起始位置，然后再来一个循环可以是for或者while，来从两个起始位置开始比较，取得重复子数组的长度。

动态规划

本题其实是动规解决的经典题目，只要想到用二维数组可以记录两个字符串的所有比较情况，这样就比较好推递推公式了。
动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j] ：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，最长重复子数组长度为dp[i][j]。（特别注意： “以下标i - 1为结尾的A” 标明一定是以A[i-1]为结尾的字符串）

那dp[0][0]是什么含义呢？总不能是以下标-1为结尾的A数组吧。

其实dp[i][j]的定义也就决定着，在遍历dp[i][j]的时候i 和 j都要从1开始。

确定递推公式

根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。

即当A[i - 1] 和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;

根据递推公式可以看出，遍历i和j要从1开始！

dp数组如何初始化

根据dp[i][j]的定义，dp[i][0]和dp[0][j]其实都是没有意义的！

但dp[i][0]和dp[0][j]要初始值，因为为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;

所以dp[i][0]和dp[0][j]初始化为0。

举个例子A[0]如果和B[0]相同的话，dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来。

确定遍历顺序

外层for循环遍历A，内层for循环遍历B。

同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。

代码如下：

for (int i = 1; i <= nums1.size(); i++) {
    for (int j = 1; j <= nums2.size(); j++) {
        if (nums1[i - 1] == nums2[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + 1;
        }
        if (dp[i][j] > result) result = dp[i][j];
    }
}

举例推导dp数组

拿示例1中，A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：

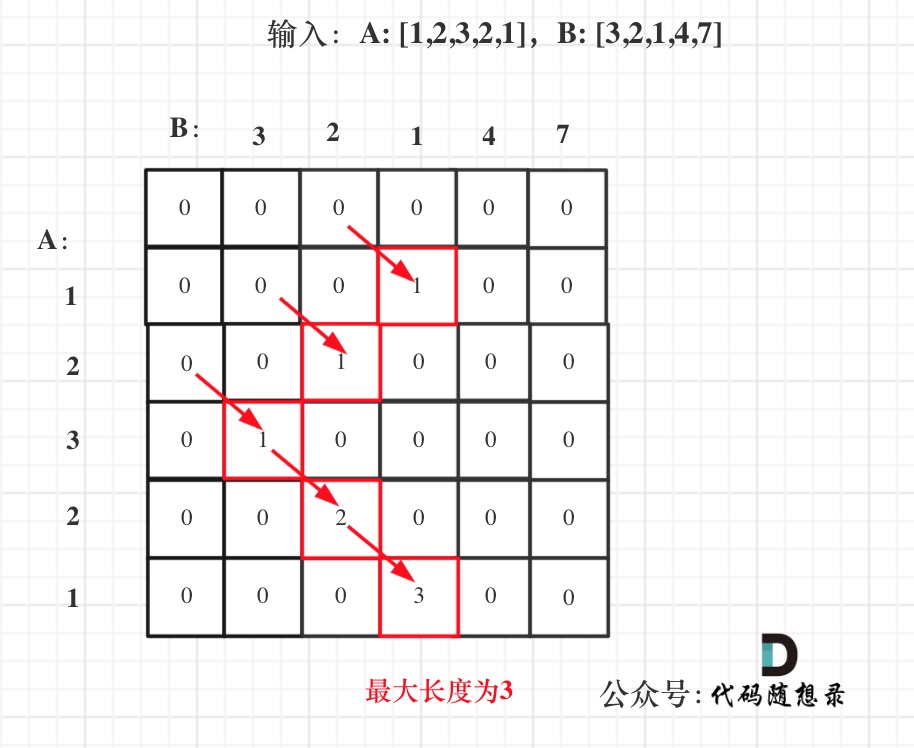
以上五部曲分析完毕，C++代码如下：

// 版本一
class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

时间复杂度：O(n × m)，n 为A长度，m为B长度
空间复杂度：O(n × m)

滚动数组

在如下图中：

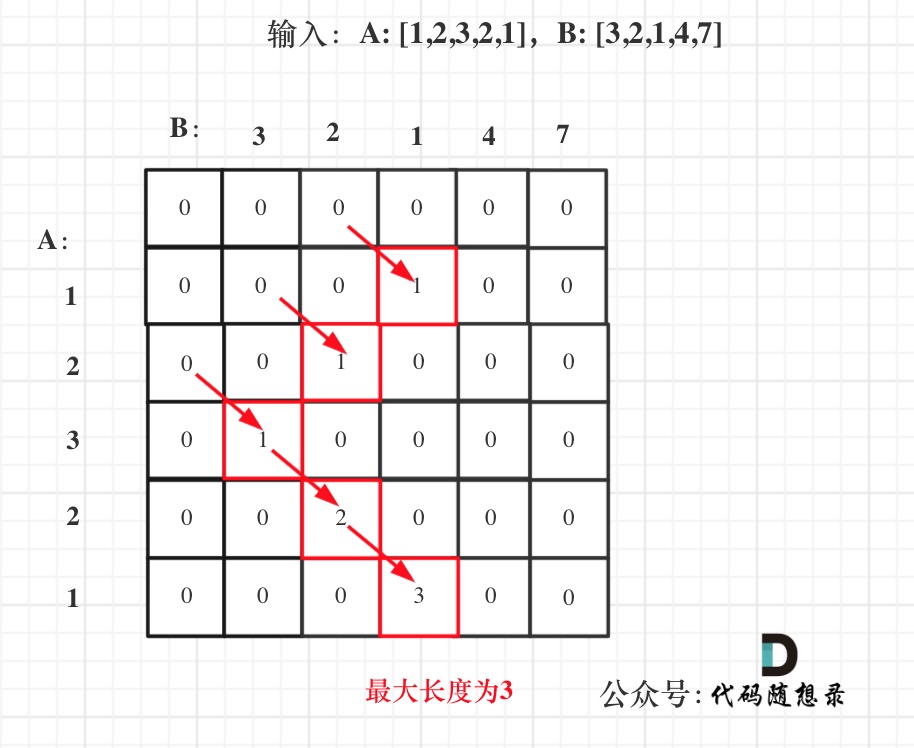
可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组，也就是dp[j]都是由dp[j - 1]推出。

也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。

此时遍历B数组的时候，就要从后向前遍历，这样避免重复覆盖。

// 版本二
class Solution {
public:
    int findLength(vector<int>& A, vector<int>& B) {
        vector<int> dp(vector<int>(B.size() + 1, 0));
        int result = 0;
        for (int i = 1; i <= A.size(); i++) {
            for (int j = B.size(); j > 0; j--) {
                if (A[i - 1] == B[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                } else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作
                if (dp[j] > result) result = dp[j];
            }
        }
        return result;
    }
};

时间复杂度：，n 为A长度，m为B长度
空间复杂度：

1143.最长公共子序列

力扣题目链接

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的公共子序列是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace”，它的长度为 3。

示例 2:

输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc”，它的长度为 3。

示例 3:

输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:

1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。

思路

本题和718. 最长重复子数组区别在于这里不要求是连续的了，但要有相对顺序，即：“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

继续动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

确定递推公式

相等情况：nums1[i - 1] == nums2[j - 1]
- 当nums1[i - 1]等于nums2[j - 1]时，表示当前元素可以构成最长公共子序列的一部分。
- 状态转移：dp[i][j] = dp[i - 1][j - 1] + 1
  - 这是因为，如果nums1[i - 1]等于nums2[j - 1]，则在dp[i-1][j-1]的基础上增加1，表示当前匹配的元素。
  - 例如，若nums1的前i-1个元素和nums2的前j-1个元素的LCS长度是dp[i-1][j-1]，那么增加一个匹配的元素后，LCS的长度为dp[i-1][j-1] + 1。
不相等情况：nums1[i - 1] != nums2[j - 1]
- 当nums1[i - 1]不等于nums2[j - 1]时，选择不包含当前元素的情况。
- 状态转移：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
  - 这表示在dp[i-1][j]和dp[i][j-1]之间取最大值。dp[i-1][j]代表不考虑nums1[i-1]，而dp[i][j-1]代表不考虑nums2[j-1]。
  - 选择更大的值意味着在不包含当前元素的情况下，能够得到的最长公共子序列长度。`

代码如下：

if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

dp数组如何初始化

先看看dp[i][0]应该是多少呢？

test1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0;

同理dp[0][j]也是0。

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

代码：

1	vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

确定遍历顺序

从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

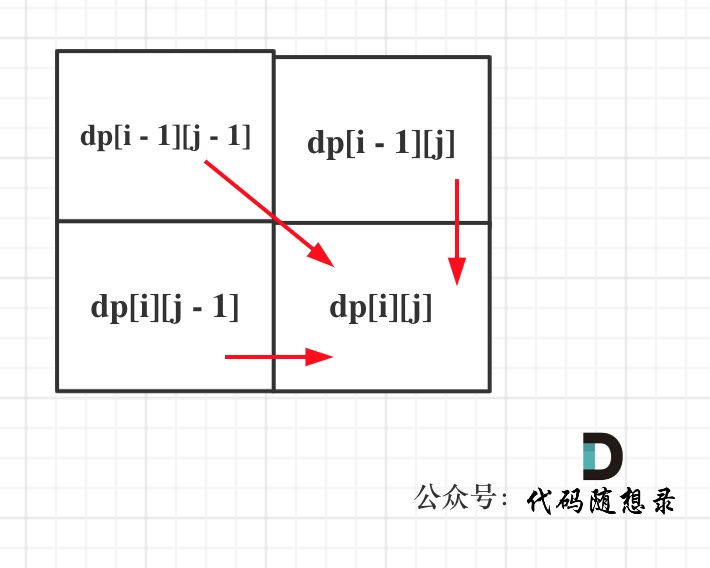
那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

举例推导dp数组

以输入：text1 = “abcde”, text2 = “ace” 为例，dp状态如图：

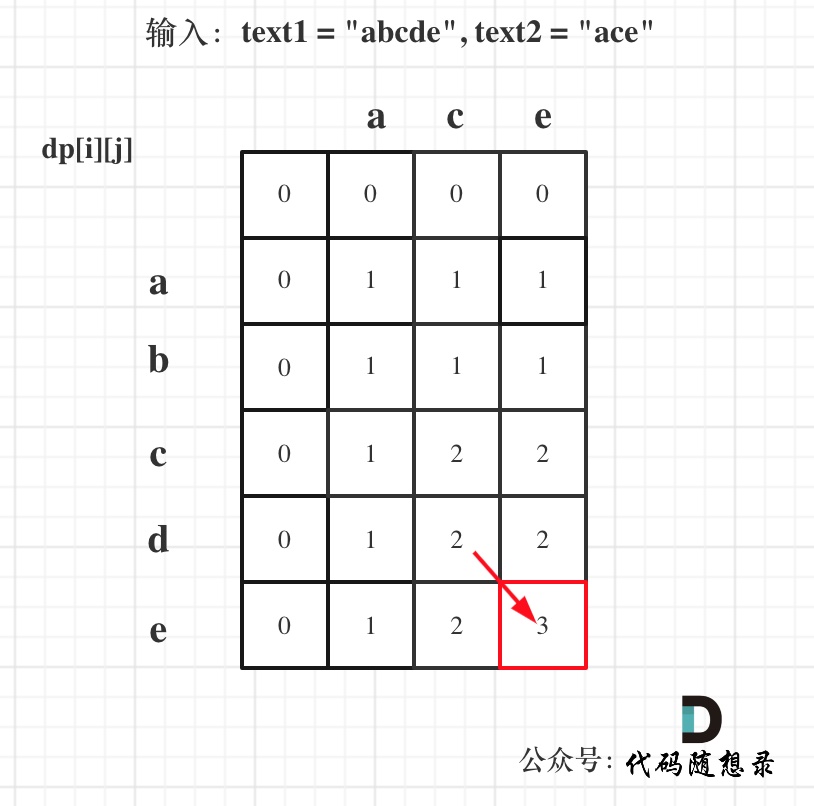
最后红框dp[text1.size()][text2.size()]为最终结果

以上分析完毕，C++代码如下：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for (int i = 1; i <= text1.size(); i++) {
            for (int j = 1; j <= text2.size(); j++) {
                if (text1[i - 1] == text2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

时间复杂度: O(n * m)，其中 n 和 m 分别为 text1 和 text2 的长度
空间复杂度: O(n * m)

1035.不相交的线

力扣题目链接

在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。

现在，可以绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且绘制的直线不与任何其他连线（非水平线）相交。

以这种方法绘制线条，并返回可以绘制的最大连线数。

思路

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。

拿示例一A = [1,4,2], B = [1,2,4]为例，相交情况如图：

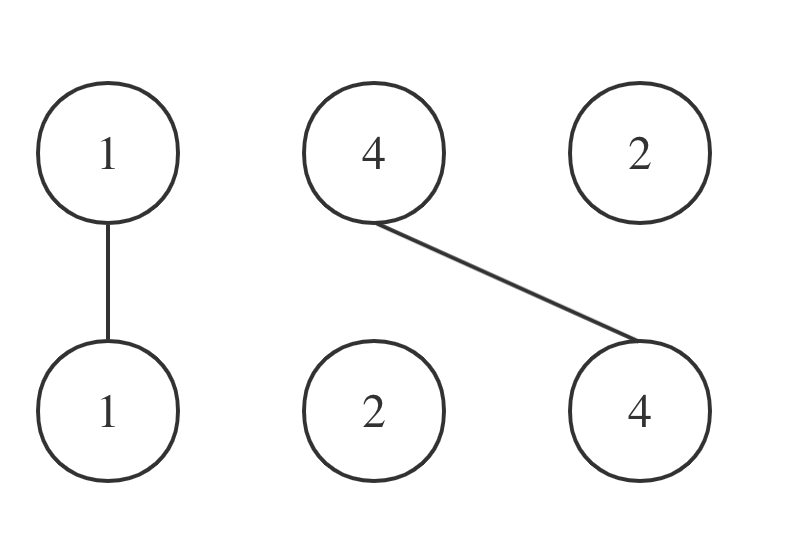
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！
那么本题就和刚刚讲过的这道题目1143.最长公共子序列就是样一样的了。

本题代码如下：

class Solution {
public:
    int maxUncrossedLines(vector<int>& A, vector<int>& B) {
        vector<vector<int>> dp(A.size() + 1, vector<int>(B.size() + 1, 0));
        for (int i = 1; i <= A.size(); i++) {
            for (int j = 1; j <= B.size(); j++) {
                if (A[i - 1] == B[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[A.size()][B.size()];
    }
};

时间复杂度: O(n * m)
空间复杂度: O(n * m)

392.判断子序列

力扣题目链接

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

示例 1：

输入：s = “abc”, t = “ahbgdc”
输出：true

示例 2：

输入：s = “axc”, t = “ahbgdc”
输出：false

提示：

0 <= s.length <= 100
0 <= t.length <= 10^4

两个字符串都只由小写字符组成。

思路

（这道题也可以用双指针的思路来实现，时间复杂度也是O(n)）

这道题应该算是编辑距离的入门题目，因为从题意中也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础。

动态规划五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。

确定递推公式

在确定递推公式的时候，首先要考虑如下两种操作，整理如下：

if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
if (s[i - 1] != t[j - 1])
- 相当于t要删除元素，继续匹配

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找到了一个相同的字符，相同子序列长度自然要在dp[i-1][j-1]的基础上加1

if (s[i - 1] != t[j - 1])，此时相当于t要删除元素，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];

其实这里可以发现和 1143.最长公共子序列的递推公式基本那就是一样的，区别就是本题如果删元素一定是字符串t，而 1143.最长公共子序列是两个字符串都可以删元素。

dp数组如何初始化

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1]和d[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。

这里大家已经可以发现，在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

因为这样的定义在dp二维矩阵中可以留出初始化的区间，如图：

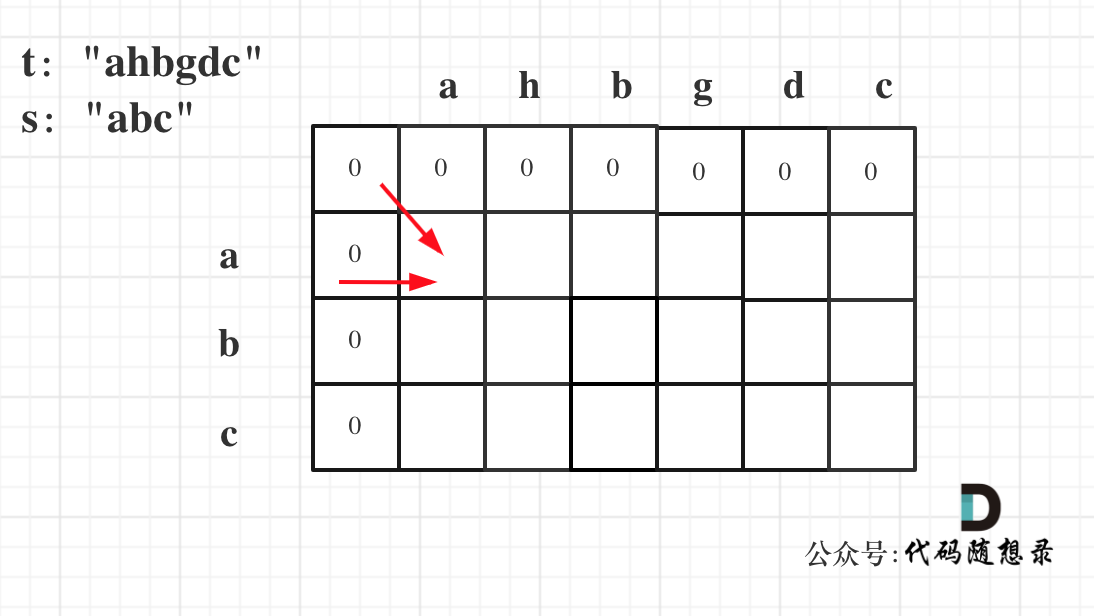
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t，初始化就比较麻烦了。

dp[i][0] 表示以下标i-1为结尾的字符串，与空字符串的相同子序列长度，所以为0. dp[0][j]同理。

1	vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));

确定遍历顺序

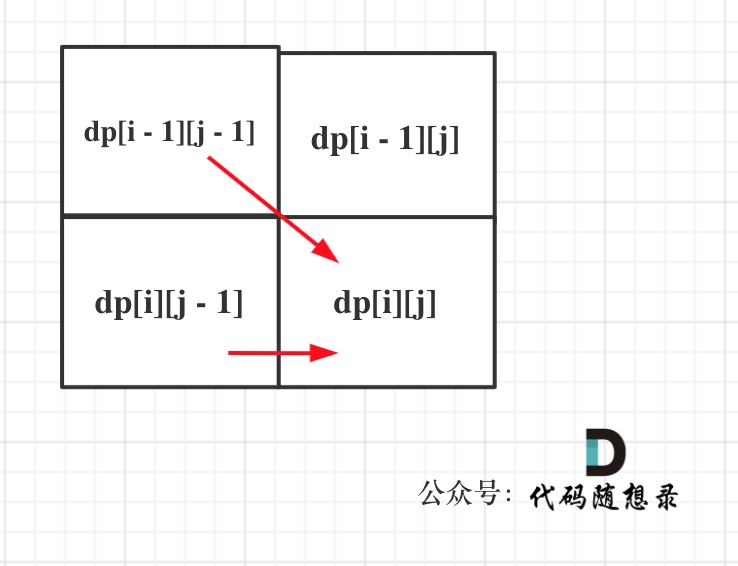
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右

如图所示：

举例推导dp数组

以示例一为例，输入：s = “abc”, t = “ahbgdc”，dp状态转移图如下：

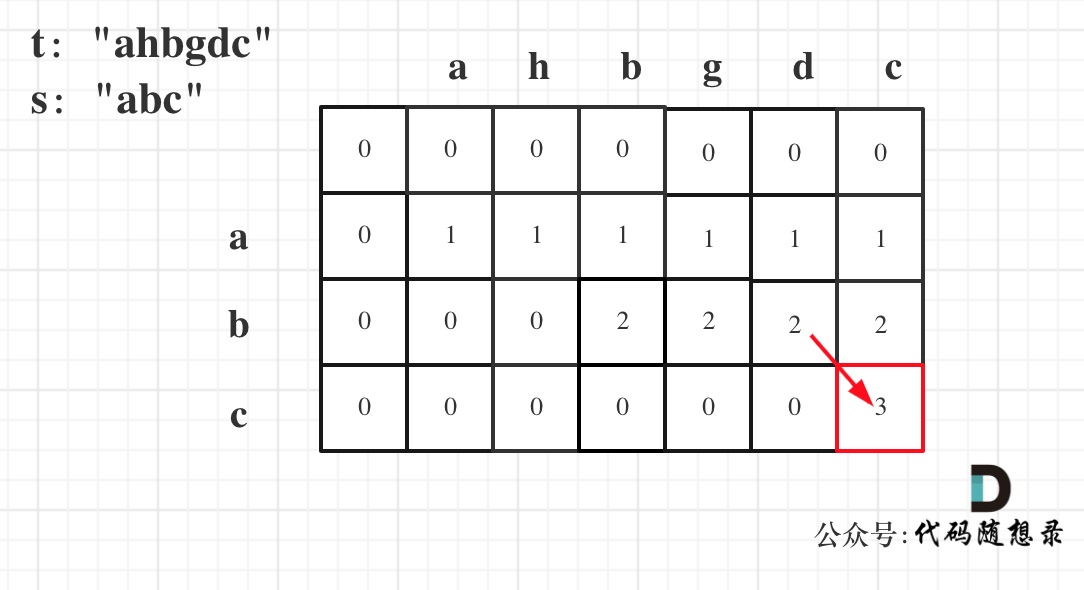
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度，所以如果dp[s.size()][t.size()] 与字符串s的长度相同说明：s与t的最长相同子序列就是s，那么s 就是 t 的子序列。

图中dp[s.size()][t.size()] = 3，而s.size() 也为3。所以s是t 的子序列，返回true。

动规五部曲分析完毕，C++代码如下：

class Solution {
public:
    bool isSubsequence(string s, string t) {
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = dp[i][j - 1];
            }
        }
        if (dp[s.size()][t.size()] == s.size()) return true;
        return false;
    }
};

时间复杂度：O(n × m)
空间复杂度：O(n × m)

总结

这道题目算是编辑距离的入门题目（毕竟这里只是涉及到减法），也是动态规划解决的经典题型。

这一类题都是题目读上去感觉很复杂，模拟一下也发现很复杂，用动规分析完了也感觉很复杂，但是最终代码却很简短。

编辑距离的题目最能体现出动规精髓和巧妙之处，大家可以好好体会一下。

115.不同的子序列

力扣题目链接

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

题目数据保证答案符合 32 位带符号整数范围。

提示：

0 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

思路

这道题目如果不是子序列，而是要求连续序列的，那就可以考虑用KMP。

这道题目相对于72. 编辑距离，简单了不少，因为本题相当于只有删除操作，不用考虑替换增加之类的。

但相对于392.判断子序列就有难度了，这道题目双指针法可就做不了了，来看看动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。

确定递推公式

这一类问题，基本是要分析两种情况

(1) s[i - 1] 与 t[j - 1]相等

使用 s[i - 1] 来匹配 t[j - 1] 时，需要考虑的是 s 的前 i - 1 个字符中找 t 的前 j - 1 个字符作为子序列的情况。即：

dp[i - 1][j - 1] 表示在 s 的前 i - 1 个字符中找到 t 的前 j - 1 个字符作为子序列的次数。

不使用 s[i - 1] 来匹配 t[j - 1] 时，只需要考虑 s 的前 i - 1 个字符中找 t 的前 j 个字符作为子序列的情况。即：

dp[i - 1][j] 表示在 s 的前 i - 1 个字符中找到 t 的前 j 个字符作为子序列的次数。

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

当然也可以用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。

所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

(2) s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成，不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j]

所以递推公式为：dp[i][j] = dp[i - 1][j];

为什么只考虑 “不用s[i - 1]来匹配” 这种情况，不考虑 “不用t[j - 1]来匹配” 的情况呢?

因为求的是 s 中有多少个 t，而不是求t中有多少个s，所以只考虑 s中删除元素的情况，即不用s[i - 1]来匹配的情况。

dp数组如何初始化

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来，如图：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。

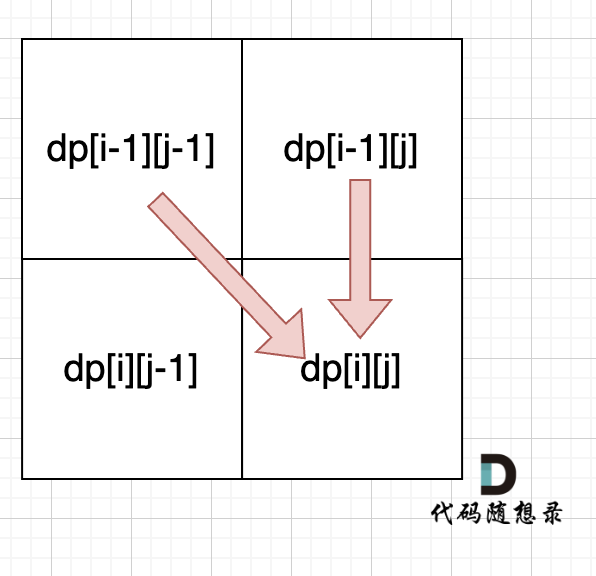
每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

初始化分析完毕，代码如下：

vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起，但为了凸显初始化的逻辑，所以还是加上了。

确定遍历顺序

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。

所以遍历的时候一定是从上到下，从左到右，这样保证dp[i][j]可以根据之前计算出来的数值进行计算。

代码如下：

for (int i = 1; i <= s.size(); i++) {
    for (int j = 1; j <= t.size(); j++) {
        if (s[i - 1] == t[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
        } else {
            dp[i][j] = dp[i - 1][j];
        }
    }
}

举例推导dp数组

假设我们有字符串 s = "rabbbit" 和 t = "rabbit"，如果我们考虑 i = 4 和 j = 2 的情况：

s 的前 4 个字符是 "rabb"。
t 的前 2 个字符是 "ra"。

现在我们看一下dp[4][2] 和 dp[3][2]：

dp[3][2] 表示在字符串 "rab" 中找到子序列 "ra" 的次数。
dp[4][2] 表示在字符串 "rabb" 中找到子序列 "ra" 的次数。

如果 s[3]（即 'b'）和 t[1]（即 'a'）不相等，那么dp[4][2] = dp[3][2]，因为我们不能用 s[3] 来匹配 t[1]，所以 dp[4][2] 只能继承 dp[3][2] 的值。

因此，dp[i - 1][j] 代表了在 s 的前 i - 1 个字符中找到 t 的前 j 个字符作为子序列的所有情况的数量。

动规五部曲分析完毕，代码如下：

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
        for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
        for (int j = 1; j < t.size(); j++) dp[0][j] = 0;
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s.size()][t.size()];
    }
};

时间复杂度:
空间复杂度:

Channing's Blog

动态规划 8️⃣

300.最长递增子序列

思路

总结

674. 最长连续递增序列

动态规划

贪心

总结

718. 最长重复子数组

思路

动态规划

滚动数组

1143.最长公共子序列

思路

1035.不相交的线

思路

392.判断子序列

思路

总结

115.不同的子序列

思路